We use the Rayleigh criterion, which states that the minimum angular separation
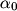 of two point sources such that ``an observer watching the images on the distant screen can just tell them apart" is, for a circular aperature with diameter of two point sources such that ``an observer watching the images on the distant screen can just tell them apart" is, for a circular aperature with diameter 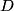 , ,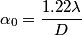 where 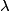 is the wavelength of the light. %(See Bekefi and Barratt pages 578 and 579). is the wavelength of the light. %(See Bekefi and Barratt pages 578 and 579). Plugging in the given value for 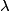 and and 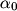 , we can find that , we can find that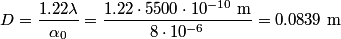 Therefore, answer (C) is correct. |